Example-Based Elastic Materials
S. Martin, B. Thomaszewski, E. Grinspun, M. GrossProceedings of ACM SIGGRAPH (Vancouver, Canada, August 7-11, 2011), ACM Transactions on Graphics, vol. 30, no. 4, pp. 72:1-72:8
Abstract
We propose an example-based approach for simulating complex elastic material behavior. Supplied with a few poses that characterize a given object, our system starts by constructing a space of prefered deformations by means of interpolation. During simulation, this example manifold then acts as an additional elastic attractor that guides the object towards its space of prefered shapes. Added on top of existing solid simulation codes, this example potential effectively allows us to implement inhomogeneous and anisotropic materials in a direct and intuitive way. Due to its example-based interface, our method promotes an art-directed approach to solid simulation, which we exemplify on a set of practical examples.Overview
Different materials deform in different ways. Therefore, physically-based animations offer control of material properties as a way of controlling the final deformation. But in creative applications such as computer animation, material properties are just middlemen in a process that really focuses on obtaining some desired deformation.
Indeed, we can flip the causality between materials and deformation: when we witness the deformation of an object, we implicitly draw conclusions about its underlying, constitutive material. By controlling the deformation of an animated object, we can imply complex material behaviors. Therefore, if we can expand the repertoire of possible deformations of an object, we can broaden the expressive palette available for physics-based computer animation.
The computational mechanics literature already describes many mathematical models for myriad materials, alas these models are intended for problems where material coefficients are easily quantified (e.g., from measurements). In artistic endeavors, we typically envision a desired deformation (the material properties are, to some extent, an afterthought - just a means to an end). Yet quantifying material coefficients that lead to a desired deformation behavior is difficult if not impossible. Indeed, just choosing a mathematical model can be daunting. Simpler models offer few coefficients but a small expressive range, while complex models have an unwieldy set of parameters.
Inspired by example-based graphical methods, we present an intuitive and direct method for artistic design and simulation of complex material behavior. Our method accepts a set of poses that provide examples of characteristic desirable deformations, created either by hand (digitized from clay sculptures), with a modeling tool, or by taking 3D "snapshots" of previously run simulations. With these examples in hand, we provide a novel forcing term for dynamical integration that causes materials to obey the "physical laws" implied by the provided examples (see Fig. 1).
Results
Global examples are used to directly specify prefered deformations for an entire object, which can be understood as a "what-you-see-is-what-you-get" approach to material design. However, there are also many common objects for which the characteristic deformations are rather local than global. Moreover, different local deformations can typically occur simultaneously and independently of each other. This kind of behavior is illustrated in the animation shown in Fig. 2, for which two characteristic deformations of a shoe, namely the buckling of its tip and the bulging of its heel, are provided as local examples to the simulation.
This animation also showcases the application of embedding: the high-resolution geometry of the shoe deforms in accordance to the coarse embedding mesh - but it does so in a very plausible way. This, in turn, is due to the fact that the volumetric example meshes were generated such that the embedded mesh assumes the desired deformations, irrespective of the actual shape of the embedding mesh.
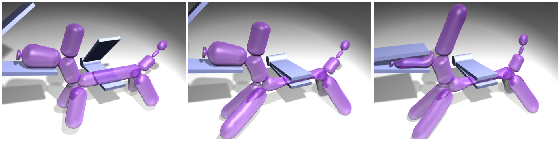
Local examples do not necessarily have to be defined over connected components, but can also couple remote regions while still affecting only a small part of the entire object. An example of this application can be seen in Fig. 3, which shows that, in an artistic setting, compressing the nose of a balloon dog can lead to an inflation of its ears.